大数据时代，数据的异常分析被广泛的用于各个场合。 今天我们就来看一看其中的一种场景，对于单变量数据集的异常检测。

所谓单变量，就是指数据集中只有一个变化的值，下面我们来看看今天我们要分析的的数据，点击这里数据文件下载数据文件。

分析数据的第一步是要加载文件， 本文使用了numpy，pandas，scikit learn等常见的数据分析要用到的Python库。

import numpy as np
import pandas as pd
df = pd.read_csv("farequote.csv")

Pandas 是一个常用的数据分析的Python库，提供对数据的加载，清洗，抽取，变形等操作。Pandas依赖numpy，numpy提供了基于列/多维数组（List/N-D Array）的数据结构的操作。许多科学计算和数据分析的库都依赖于numpy。

df 是Pandas中常用的数据类型dataframe，dataframe类似与一个数据库的表，使用 df.head()可以得到数据的头几行，以便了解数据的概貌。

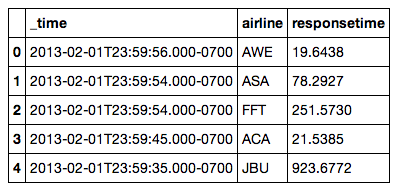
该数据结构中，第一列式Pandas添加的索引，第一行是每一列数据的名字，除了第一列，每一列数据可以看成是一个变量，所以该数据集共有三个变量，时间（_time）、航空公司名称(airline)、响应时间（responsetime）。我们可以这样理解，该数据集记录了一段时间内，各个航空公司飞机延误的时间。我们希望通过分析找出是否存在异常的情况。

注意，我们是要分析单变量，所以所有的分析都是基于某一个航空公司的数据，所以就需要对该数据集做一个查询，找出要分析的航空公司。首先要知道有哪些航空公司，使用np.unique(df.airline)可以找到所有的航空公司代码，类似SQL的Unique命令

array(['AAL', 'ACA', 'AMX', 'ASA', 'AWE', 'BAW', 'DAL', 'EGF', 'FFT',
       'JAL', 'JBU', 'JZA', 'KLM', 'NKS', 'SWA', 'SWR', 'TRS', 'UAL', 'VRD'], 
      dtype='|S3')

查询某个航空公司的数据使用dataframe的query方法，类似SQL的select。Query返回的结果仍然是一个dataframe对象。

dd = df.query('airline=="KLM"') ## 得到法航的数据

我们先了解一下数据的大致信息，使用describe方法

dd.responsetime.describe()

得到如下的结果：

count    1724.000000
mean     1500.613766
std       100.085320
min      1209.766800
25%      1434.084625
50%      1499.135000
75%      1567.831025
max      1818.774100
Name: responsetime, dtype: float64

该结果返回了数据集responsetime维度上的主要统计指标，个数，均值，方差，最大最小值等等，也可以调用单独的方法例如min（），mean（）等来获得某一个指标。

基于标准差得异常检测

下面我们就可以开始异常点的分析了，对于单变量的异常点分析，最容易想到的就是基于标准差（Standard Deviation）的方法了。我们假定数据的正态分布的，利用概率密度函数，我们知道

• 95.449974面积在平均数左右两个标准差的范围内

• 99.730020%的面积在平均数左右三个标准差的范围内

• 99.993666的面积在平均数左右三个标准差的范围内

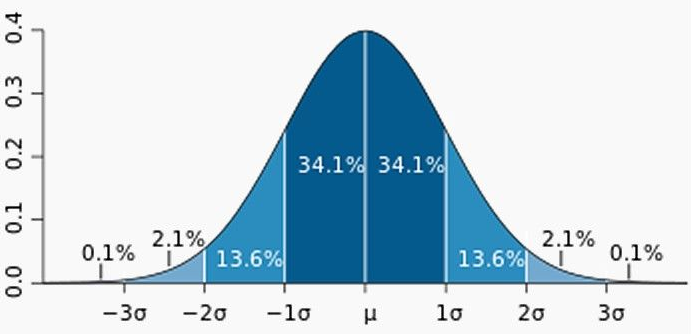
所以我们95%也就是大概两个标准差为门限，凡是落在门限外的都认为是异常点。代码如下

def a1(dataframe, threshold=.95):
    d = dataframe['responsetime']
    dataframe['isAnomaly'] = d > d.quantile(threshold)  
    return dataframe
print a1(dd)

运行以上程序我们得到如下结果

                             _time airline  responsetime isAnomaly
20    2013-02-01T23:57:59.000-0700     KLM     1481.4945     False
76    2013-02-01T23:52:34.000-0700     KLM     1400.9050     False
124   2013-02-01T23:47:10.000-0700     KLM     1501.4313     False
203   2013-02-01T23:39:08.000-0700     KLM     1278.9509     False
281   2013-02-01T23:32:27.000-0700     KLM     1386.4157     False
336   2013-02-01T23:26:09.000-0700     KLM     1629.9589     False
364   2013-02-01T23:23:52.000-0700     KLM     1482.5900     False
448   2013-02-01T23:16:08.000-0700     KLM     1553.4988     False
511   2013-02-01T23:10:39.000-0700     KLM     1555.1894     False
516   2013-02-01T23:10:08.000-0700     KLM     1720.7862      True
553   2013-02-01T23:06:29.000-0700     KLM     1306.6489     False
593   2013-02-01T23:03:03.000-0700     KLM     1481.7081     False
609   2013-02-01T23:01:29.000-0700     KLM     1521.0253     False
666   2013-02-01T22:56:04.000-0700     KLM     1675.2222      True
...   ...   ...   ...

结果数据集上多了一列isAnomaly用来标记每一行记录是否是异常点，我们看到已经有一些点被标记为异常点了。

我们看看程序的详细内容：

1. 方法a1定义了一个异常检测的函数

2. dataframe['responsetime']等价于dataframe.responsetime,该操作取出responsetime这一列的值

3. d.quantile(threshold)用正态分布假定返回位于95%的点的值，大于该值得点都落在正态分布95%之外

4. d > d.quantile(threshold)是一个数组操作，返回的新数组是responsetime和threshold的比较结果，[False,False,True,... ... False]

5. 然后通过dataframe的赋值操作增加一个新的列，标记所有的异常点。

数据可视化往往是数据分析的最后一步，我们看看结果如何：

import matplotlib.pyplot as plt
da = a1(dd)
fig = plt.figure()
ax1 = fig.add_subplot(2, 1, 1)
ax2 = fig.add_subplot(2, 1, 2)
ax1.plot(da['responsetime'])
ax2.plot(da['isAnomaly'])

这异常点也太多了，用99%在试试：

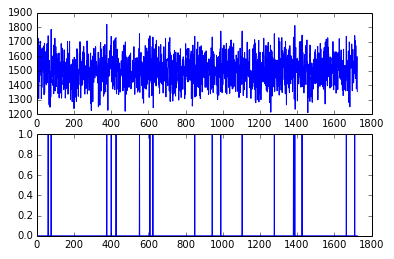
现在似乎好一点，然而我们知道，对于数据集的正态分布的假定往往是不成立的,假如数据分布在大小两头，那么这样的异常检测就很难奏效了。我们看看其他一些改进的方法。

基于ZSCORE的异常检测

zscore的计算如下

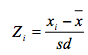
sd是标准差，X是均值。一般建议门限值取为3.5

代码如下：

def a2(dataframe, threshold=3.5):
    d = dataframe['responsetime']
    zscore = (d - d.mean())/d.std()
    dataframe['isAnomaly'] = zscore.abs() > threshold
    return dataframe

另外还有一种增强的zscore算法，基于MAD。MAD的定义是

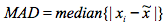
其中X是中位数。

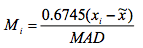
增强的zscore算法如下：

def a3(dataframe, threshold=3.5):
    dd = dataframe['responsetime']
    MAD = (dd - dd.median()).abs().median()
    zscore = ((dd - dd.median())* 0.6475 /MAD).abs()
    dataframe['isAnomaly'] = zscore > threshold
    return dataframe

用zscore算法得到：

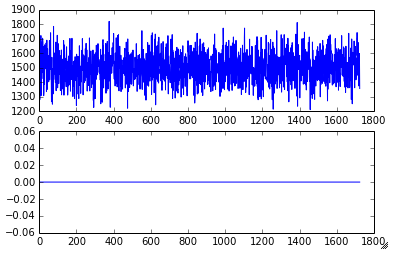
调整门限为3得到

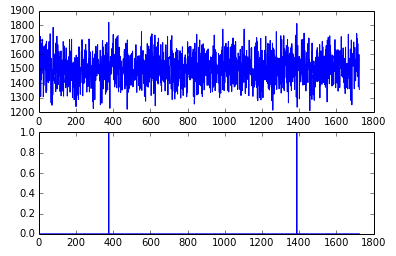
如果换一组数据AAL，结果会怎么样呢?

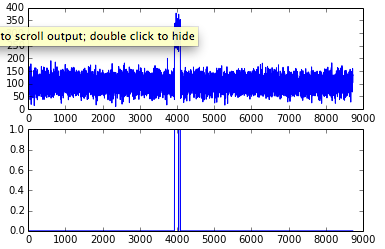
我们发现有一段时间，所有的响应都很慢，我们想要把这些点都标记为异常，可能么？

基于KMEAN聚集的异常检测

通常基于KMEAN的聚集算法并不适用于异常点检测，以为聚集算法总是试图平衡每一个聚集中的点的数目，所以对于少数的异常点，聚集非常不好用，但是我们这个例子中，异常点都聚在一起，所以应该可以使用。

首先，为了看清聚集，我们使用时间序列的常用分析方法，增加一个维度，该维度是每一个点得前一个点得响应时间。

preresponse = 0
newcol = []
newcol.append(0)
for index, row in dd.iterrows():
    if preresponse != 0:
        newcol.append(preresponse)
    preresponse = row.responsetime
dd["t0"] = newcol
plt.scatter(dd.t0,dd.responsetime)

我们利用iterrows来循环数据，把前一个点的响应时间增加到当前点，第一个点的该值为0，命名该列为t0。然后用scatter plot把它画出来。

上面是法航KLM的数据，其中最左边的点是一个无效的点，因为前一个点的响应时间不知道所以填了0，分析时应该过滤该店。

对于AAL，我们可以清楚的看到两个聚集：

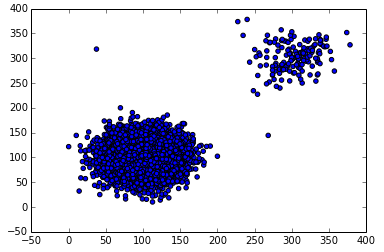
其中右上方的聚集，也就是点数目比较少得聚集就是我们希望检测到的异常点得集合。

我们看看如何使用KMEAN算法来检测吧：

def a4(dataframe, threshold = .9):
    ## add one dimention of previous response
    preresponse = 0
    newcol = []
    newcol.append(0)
    for index, row in dataframe.iterrows():
        if preresponse != 0:
            newcol.append(preresponse)
        preresponse = row.responsetime
    dataframe["t0"] = newcol
    ## remove first row as there is no previous event for time
    dd = dataframe.drop(dataframe.head(1).index) 
    clf = cluster.KMeans(n_clusters=2)
    X=np.array(dd[['responsetime','t0']])
    cls = clf.fit_predict(X)
    freq = itemfreq(cls)
    (A,B) = (freq[0,1],freq[1,1])
    t = abs(A-B)/max(A,B)
    if t > threshold :
        ## "Anomaly Detected!"
        index = freq[0,0]
        if A > B :
            index = freq[1,0]
        dd['isAnomaly'] = (cls == index)
    else :
        ## "No Anomaly Point"
        dd['isAnomaly'] = False
    return dd

其核心代码是以下这几行：

clf = cluster.KMeans(n_clusters=2)
X=np.array(dd[['responsetime','t0']])
cls = clf.fit_predict(X)

cluster.KMeans返回一个预测模型，我们假定有两个聚集。你可以试着加大聚集的数量，结果没什么影响。

dd[['responsetime','t0']]返回一个2*n的数组，并赋值给X，用于聚集计算。

fit_pridict方法是对X做聚集运算,并计算每一个点对应的聚集编号。

freq = itemfreq(cls)

itemfreq返回聚集结果中每一个聚集的发生频率，如果其中一个比另一个显著地多，我们则认为那个少得是异常点聚集。

用该方法可以把所有聚集里的点标记为异常点。

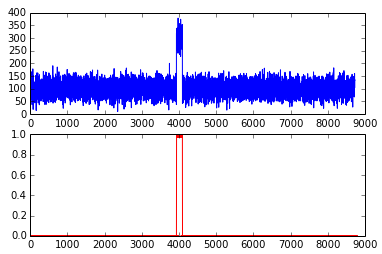
这里我用红色标记结果让大家看的清楚一点，注意因为是line chart，连个竖线间的都是异常点。

总结

除了上述的算法，还有其它一些相关的算法，大家如果对背后的数据知识有兴趣的话，可以参考这篇相关介绍。

单变量的异常检测算法相对比较简单，但是要做到精准检测就更难，因为掌握的信息更少。另外boxplot也经常被用于异常检测，他和基于方差的异常检测是一致的，只不过用图形让大家一目了然的获得结果，大家有兴趣可以了解一下。

[取消回复评论]

昵称 登录 E-mail: *
Web:
Twitter:

当有新评论通过 E-mail 通知我

(输入验证码)

or Ctrl+Enter